本期作者

Yvette Zheng

投资评估中实物期权的应用

前言

实物期权(real options)的概念最初是1977年由著名金融学家StewartMyers在MIT时提出的，他指出一个投资项目所创造的利益，来自于截止到目前所拥有资产的使用，再加上一个对未来投资机会的选择。也就是说企业可以取得一个权利，在未来以一定价格取得或出售一项实物资产或投资计划，所以实物资产的投资可以用类似于评估一般期权的方式来进行评估。同时又因为其标的物为实物资产，故将此性质的期权称为实物期权。

实物期权是P4考纲Part B的一部分，根据考纲，考生需要对一个项目中包含的实物期权进行分类以及评估。要求的知识水平是级别3，即Professional level专业水平。实物期权在历年考题June 2011 Q4、June 2012 Q1、Dec 2013 Q1、June 2014 Q4以及March 2016 Q4中考察过，同学们可以找出来练练手。

介绍

实物期权估值方法弥补了传统净现值法项目评估的不足，考虑了现实中的灵活性和选择性。本文通过三个例子讲解了如何将实物期权纳入投资评估当中，实物期权在实际应用中的局限性，以及如何减轻局限性。

NET PRESENTVALUE(NPV)AND REAL OPTIONS净现值法以及实物期权

传统NPV方法假设的是一个投资项目从零时刻（即现在）开始，并按照最初的预期完成。因此，它假设企业的管理层必须现在马上做出决策，决定执行还是永不执行该项目。一旦决定，就不能改变。而实际上大多数投资决策都是具有灵活性的，可以让管理层选择采取何种行动。

实物期权是在净现值不确定的情况下，例如企业:

■有权推迟决策，而不需要现在决定执行或是永不执行项目

■制定和实施决策之后还有权可以改变

■有权对初始投资的项目进一步开发

因此，当企业在决策中具有一定的灵活性，或者即使做出决定，未来还是可以改变，本质上就是存在着期权。企业可以利用这个权力改变初始的决策，因此这个权力，即期权具有一定的价值。实物期权的估值方法评估了当管理人员决定是否要进行项目时，所存在的灵活性和选择性的价值。

传统NPV中，与项目相关的风险和不确定性是在资本成本中考虑的，并通过对离散结果的概率分析以及敏感性分析或压力测试分析。而期权，是从另一个角度出发，将风险和不确定性视为机遇，企业有权开发有利的趋势，而抵制负面的影响。

期权方法考虑了制定决策之前的时间，以及所附带的风险和不确定性。通过使用这些因素来估算一个额外的可归算于项目的价值。

ESTIMATING THEVALUE OF REAL OPTIONS估算实物期权的价值

实际中有很多类型的实物期权，在P4考试中，根据考官，考生需要解释并计算出下面总结的三种实物期权的价值：

■Optionto delay-将决策推迟到未来日期的期权（看涨期权）

■Optionto abandon-当继续进行项目不利的情况下，放弃该项目的期权（看跌期权）

■Optionto expand–通过初始项目可能产生后续机会的期权（看涨期权）

而对于option to redeploy–用于项目的资产可以转换到其他项目或活动中的期权，考生仅要求能够解释，但不要求计算。

对于P4考试，我们可以假设实物期权是欧式期权，也就是在未来某一特定时间可以行使的权力，那么可以通过Black-Scholes Option Pricing（BSOP）模型以及put-call parity来估算期权的价值。然而，因为这是假设，可能无法估算出期权的真实价值(参见下面的局限和假设部分)。

使用BSOP模型计算实物期权的价值时，需要用到5个变量：

➀Pa-标的资产价值，它是项目产生的未来现金流的现值。

➁Pe-行权价格，是指在行使期权时所支付的金额，或在期权执行时收到的金额。

➂r-无风险利率，通常根据短期政府票据回报率，得到的往往是离散利率，而BSOP模型中应使用连续复利。对于P4考试，在估算实物期权的价值时，可以假定连续和离散的利率是相同的。

➃s-波动率，是指由标准偏差所度量的项目或标的资产的风险。

➄t–行权期，是由年数度量的时间，指的是在期权结束之前可以行使的时间。

下面三个示例讲解了如何使用BSOP模型来估算三种类型的实物期权的价值。在这三个例子中，N(d1)和N(d2)的数字都是按照考试提供的Standard Normal Distribution Table标准正态分布表来计算实物期权的价值。

Example 1：Option to delay

一家公司正在考虑竞标项目的专有权，该项目最初将耗资$35m。

公司预测，接下来四年的项目现金流如下:

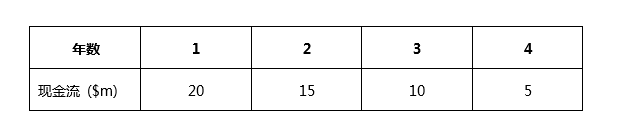
该项目的相关资本成本为11%，无风险利率为4.5%。现金流的波动率(标准差)估计为50%。

解答：

不考虑optionto delay下的NPV为：

NPV=$5.8m

假设公司不需要现在做出决定，可以延迟两年才做出决定。

考虑了选择延迟两年决策之后的NPV：

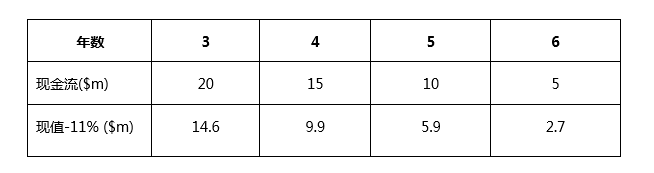
BSOP模型中用到的变量：

标的资产价值Pa=$14.6m+$9.9m+$5.9m+$2.7m=$33.1m

行权价格Pe=$35m

行权期t=2年

无风险利率r=4.5%

波动率s=50%

运用BSOP模型计算出：

从StandardNormal Distribution Table中可以找出，N(d1)=0.6554，N(d2)=0.3783

由于optionto delay本质上是call option，其价值可以估算为：

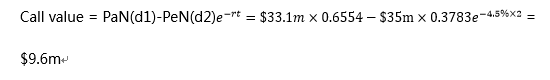
由于公司可以延迟两年再决定，并且波动性较大，这个项目的专有权可以标价$9.6m，而不是$5.8m。价值的增加反映了做出决定之前的时间和现金流的波动性。

Example 2:Option to expand

一家公司正在考虑投资一个项目，该项目的净现值为$3m，但这个项目有可能利用为初始项目开发的技术进行进一步扩张。这一扩张将涉及在4年内完成的第二个项目。目前，第二个项目现金流的现值估计为$90m，预计4年的费用估计为$140m。项目现金流的标准偏差可能为40%，而目前的无风险回报率为5%。

解答：

第二个(后续)项目BSOP模型中使用的变量如下:

标的资产价值Pa=$90m

行权价格Pe=$140m

行权期t=4年

无风险利率r=5%

波动率s=40%

运用BSOP模型计算出：

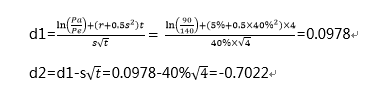
从Standard Normal Distribution Table中可以找出，N(d1)=0.5398，N(d2)=0.2420

由于option to expand本质上是call option，其价值可以估算为：

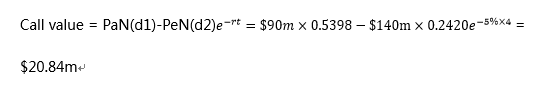
当两个项目同时考虑时，整体价值为$23.84m（$3m+$20.84m）。目前，与第二个项目产生的现金流现值相比，$140m的成本相当大，再加上传统的NPV可能会计算出第二个项目的NPV为负，因此公司很有可能也不会开展第一个项目。然而，在确定是否要进行第二个项目之前还有4年的时间。在这段时间里面，由于高波动率，现金流可能会发生很多变化。公司可以用$23.84m的价值决定是否投资于第一个项目，或者是否应该将资金投资于其他活动。又或者可以考虑以$23.84m的价格出售这两个项目的权力。

Example 3:Option to abandon

Duck Co正在考虑一个为期五年的项目，初始成本为$37.5m，估计项目现金流的现值如下:

Swan Co联系了Duck Co，并提出在第三年年初以$28m的价格收购整个项目。无风险回报率为4%。Duck Co的财务总监认为，该项目存在许多不确定性，并评估现金流可能因这些不确定性而产生35%的标准偏差。

解答：

Swan Co的报价可以认为是Duck Co的一个实物期权，因为它提供了一个出售项目，即放弃项目的权力。看跌期权价值是基于标准偏差的评估和BSOP模型，以及put-call parity公式计算的。

虽然Duck Co实际上不会从SwanCo的报价中获得即时现金流，但通过下面的实物期权计算可以看出，该项目是值得进行的，因为波动可能导致未来现金流的增加。

不考虑optionto abandon下的NPV为：

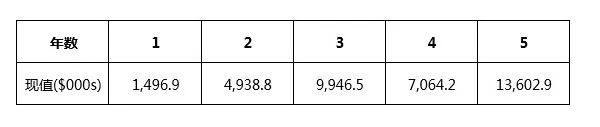
现金流现值=$37,049,300

初始投资金额=$37,500,000

项目净现值NPV=$37,049,300-$37,500,000=$(450,700)

考虑optionto abandon下的NPV为：

标的资产价值Pa=$9.9m+$7.1m+$13.6m=$30.6m（第三年年初之后的现金流现值）

行权价格Pe=$28m

行权期t=2年（第三年年初，即第二年结束，所以t=2）

无风险利率r=4%

波动率s=35%

运用BSOP模型计算出：

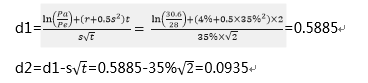
从Standard Normal Distribution Table中可以找出，N(d1)=0.7224，N(d2)=0.5359

由于option to abandon本质上是put option，其价值可以估算为：

考虑了实物期权的价值后，项目的净现值大约为$3.05m($3.50-$0.45m)。

如果没有考虑Swan Co的报价，那么这个项目会得出一个边际负净现值，当然敏感性分析的结果也需要同时考虑。如果仅将原始结果考虑在内，公司应该不会继续进行这个项目。然而，在考虑到Swan Co的报价和不确定性之后，项目的净现值是正的。这表明Duck Co应该进行该项目。

LIMITATIONS ANDASSUMPTIONS局限性及假设

下面讨论的许多限制和假设主要都是由于，我们运用了一个由金融产品开发的模型（BSOP模型）来对实物和长期投资的灵活性和选择性进行估值。

欧式期权或美式期权

BSOP模型是二项模型的简化，它假设实物期权是欧式期权，只能在期权到期的时候执行权力。美式期权可以在到期日之前任何时候行使。实际上，大多数的期权，无论是实物的还是金融的，都是美式期权。

在许多情况下，欧式期权和同类的美式期权的价值基本上是相同的，因为除非期权的标的资产是在期权到期之前获得部分收益，否则提早行使期权是无法得到任何好处的。到期前的期权会有一个附加的时间价值，这意味着如果期权被执行的话，期权到期前的期权价值比期权的内在价值要大。

然而，如果期权的标的资产是在期权到期之前可以获得部分收益，举例来说，股票的股息支付，提早行使期权有可能是有益的。对于实物期权，同样的道理，竞争对手的某些行为可能会使得提前行使期权更有利。在这种情况下，美式期权的价值将高于同类的欧式期权。

由于这些原因，通过BSOP模型得出来的结果，要么低估了一个期权的价值，要么给出一个接近其真实情况的价值。总体来说，估算一个项目中内在的实物期权并加到项目的净现值中，会使得项目的价值评估更加准确，从而减少企业投资不足的倾向。

估算波动率

BSOP模型假设标的资产的波动率或风险可以简单并准确地确定。对于交易的金融资产来说，这确实是事实，因为可以通过历史数据来评估标的资产的波动性，但实物期权却很难做到。实物期权大多数情况是通过大型的一次性项目而取得，而这些项目很少或者没有可用的历史数据。

这种情况下的波动率需要通过模拟来估算，例如蒙特卡罗模拟模型，但需要确保模型运用准确并且输入的数据合理地反映了实际情况下可能发生的情况。

其他局限性

BSOP模型需要对模型中使用的变量做出假设，主要包括：

(a)BSOP模型假设标的项目或资产是在完全市场的情况下进行交易的。在这种情况下，资产的信息是可以自由获取的，并且正确反映在资产价值中。此外，它假设存在一个市场，可以不受限制地交易标的项目或资产(也就是说，市场是无阻力的)。

(b)BSOP模型假设利率和标的资产波动保持不变，直到到期结束。此外，它假设可以准确估计到期时间。

(c)BSOP模型假设项目和资产的现金流遵循对数正态分布，类似于股票市场，这是由于这个模型是基于股票市场研发出来的。

(d)BSOP模型没有考虑到行为金融学的因素，管理者在做决策时可能表现出来某些行为异常，比如过度乐观。

(e)BSOP模型假设在构建期权时，所约定好的涉及双方未来承诺的合同义务，将具有约束力，并将得到满足。例如，在上面的例子中，假设了Swan Co会履行承诺，两年后以$28m的价格向Duck Co购买项目，并没有考虑不履行该承诺的风险。

在实际中，这些假设中可能会有一个或多个不适用。因此BSOP模型无法真正提供一个“正确”的价值，而是为项目将来的选择和灵活性提供了一个“指示性”的价值。

总结

本文讨论了如何将实物期权的因素加入到投资评估决策中，特别是考虑了管理层在做投资决策时附加的灵活性和选择的价值。然后通过使用BSOP模型计算三种实物期权的情况。接着还讨论了将BSOP模型应用到实物期权计算时的局限性和假设。因此，通过BSOP模型计算出的价值是指示性的，而不是绝对准确的。

      点击在线咨询泽稷老师，ACCA中文宝典免费领，更有机会获得海量免费ACCA学习资料。